Machine learning - Regression - Simple Linear Regression
Simple linear regression es una ecuacion de primer grado. Para calcular los mejores coeficientes usa el metodo Ordinary least squares
y=b + cx - y variable dependiente - b constant y-intercept - c slope coeficient - x variable independiente
Importing the libraries
import numpy as np # trabajo con arrays import matplotlib.pyplot as plt # para hacer gráficos import pandas as pd # importar los datasets, la matriz de características y el vector de variable dependiente
Importing the dataset
dataset = pd.read_csv('Data.csv') # cargo el dataset
print(dataset)
YearsExperience Salary
0 1.1 39343.0
1 1.3 46205.0
2 1.5 37731.0
3 2.0 43525.0
4 2.2 39891.0
5 2.9 56642.0
6 3.0 60150.0
7 3.2 54445.0
8 3.2 64445.0
9 3.7 57189.0
10 3.9 63218.0
11 4.0 55794.0
12 4.0 56957.0
13 4.1 57081.0
14 4.5 61111.0
15 4.9 67938.0
16 5.1 66029.0
17 5.3 83088.0
18 5.9 81363.0
19 6.0 93940.0
20 6.8 91738.0
21 7.1 98273.0
22 7.9 101302.0
23 8.2 113812.0
24 8.7 109431.0
25 9.0 105582.0
26 9.5 116969.0
27 9.6 112635.0
28 10.3 122391.0
29 10.5 121872.0
X = dataset.iloc[:, :-1].values # pongo en el panda dataset X todas las filas de todas las columnas menos la última porque en ella está la variable dependiente
y = dataset.iloc[:, -1].values # pongo en el panda dataset y todas las filas de la ultima columna
print(X)
[[ 1.1]
[ 1.3]
[ 1.5]
[ 2. ]
[ 2.2]
[ 2.9]
[ 3. ]
[ 3.2]
[ 3.2]
[ 3.7]
[ 3.9]
[ 4. ]
[ 4. ]
[ 4.1]
[ 4.5]
[ 4.9]
[ 5.1]
[ 5.3]
[ 5.9]
[ 6. ]
[ 6.8]
[ 7.1]
[ 7.9]
[ 8.2]
[ 8.7]
[ 9. ]
[ 9.5]
[ 9.6]
[10.3]
[10.5]]
print(y)
[ 39343. 46205. 37731. 43525. 39891. 56642. 60150. 54445. 64445.
57189. 63218. 55794. 56957. 57081. 61111. 67938. 66029. 83088.
81363. 93940. 91738. 98273. 101302. 113812. 109431. 105582. 116969.
Splitting the dataset into the Training set and Test set
Se suelen crear 4 datasets - X_train 66% para entrenar el modelo - Y_train las respuestas de X_train - X_test 33% para comprobar el modelo - Y_test las respuestas del modelo from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 1/3, random_state = 0) #0.33 dedico el 33% a test print(X_train) [ 2.9] [ 5.1] [ 3.2] [ 4.5] [ 8.2] [ 6.8] [ 1.3] [10.5] [ 3. ] [ 2.2] [ 5.9] [ 6. ] [ 3.7] [ 3.2] [ 9. ] [ 2. ] [ 1.1] [ 7.1] [ 4.9] [ 4. ]] print(X_test) [[ 1.5] [10.3] [ 4.1] [ 3.9] [ 9.5] [ 8.7] [ 9.6] [ 4. ] [ 5.3] [ 7.9]] print(y_train) [ 56642. 66029. 64445. 61111. 113812. 91738. 46205. 121872. 60150. 39891. 81363. 93940. 57189. 54445. 105582. 43525. 39343. 98273. 67938. 56957.] print(y_test) [ 37731. 122391. 57081. 63218. 116969. 109431. 112635. 55794. 83088. 101302.]
Training the Simple Linear Regression model on the Training set
from sklearn.linear_model import LinearRegression # importo la clase LinearRegression de la libreria sklearn del modulo linear_model regressor = LinearRegression() # creo un objeto de la clase LinearRegression regressor.fit(X_train, y_train) # fit = entreno el modelo con los datasets de train
Predicting the Test set results
y_pred = regressor.predict(X_test) # obtengo los resultados de X_test
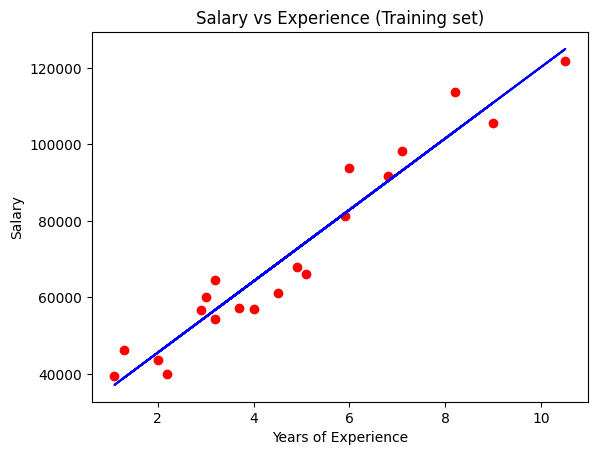
Visualising the Training set results
plt.scatter(X_train, y_train, color = 'red') # dibujo en puntos rojos los datos de training
plt.plot(X_train, regressor.predict(X_train), color = 'blue') # dibujo en azul el modelo
plt.title('Salary vs Experience (Training set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show()
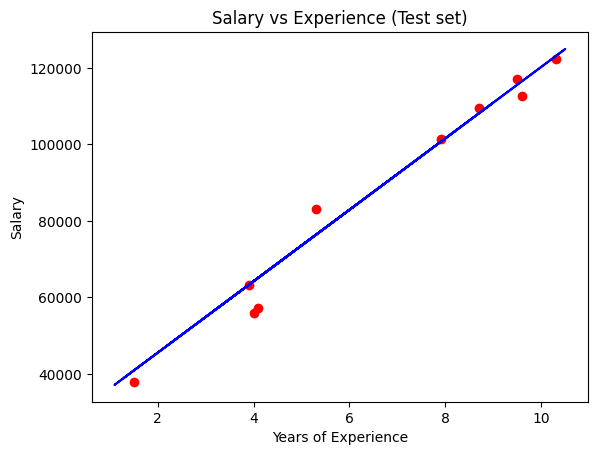
Visualising the Test set results
plt.scatter(X_test, y_test, color = 'red') # dibujo enrojo los datos de testeo
plt.plot(X_train, regressor.predict(X_train), color = 'blue') # dibujo en azul el model,uso X_train porque el modelo es el mismo que para X_test
plt.title('Salary vs Experience (Test set)')
plt.xlabel('Years of Experience')
plt.ylabel('Salary')
plt.show()
Making a single prediction (for example the salary of an employee with 12 years of experience)
print(regressor.predict([[12]])) # los 2 [[ es porque el modelo espera un array de 2 dimensiones [138967.5015615]
Getting the final linear regression equation with the values of the coefficients
print(regressor.coef_) print(regressor.intercept_) [9345.94244312] 26816.192244031183 Así que el modelo queda Salario = egressor.coef_ x YearsOfExperenia + regressor.intercept_ Salario = 9345.94244312 x YearsOfExperenia + 26816.192244031183